深入理解圆方树

发表于 | 分类于 | 阅读次数:
在五月份时我写过《仙人掌问题的处理方法》一文，现在看来，当时的做法大多是效率低、迁移性差的 DP ，其中涉及圆方树的部分也没有谈到其精髓，且当时受限于代码能力很多神题都没有自己实现。因此博主决定在写一篇博客较为深入地交流一下我对圆方树的理解。虽然本人蒟蒻目前没有能力有限，难以对仙人掌的简便做法和高深算法有什么研究，但是希望我的工作能为看似高大上的仙人掌走入广大 OI 初学者的视野、最终使仙人掌普及至 NOIP 选手中去的伟大事业做出贡献。说到底，仙人掌对于锻炼代码能力、调试能力，巩固图论、动态规划知识还是有很大作用的。

##概念及实现

仙人掌最短路

虚仙人掌

树上有一类问题可以通过建虚树解决，它们的共同特征是部分节点的树上动规问题，询问数通常很多，但是所有询问的点数之和与总点数是同一数量级的。在树上的话就可以每次建一颗虚树快速解决，参考我之前的博客虚树，而我们把仙人掌建成圆方树之后也可以按照相同的方法处理。

不过直接套用之前的方法肯定是不行的，我们需要对环上的情况进行特殊处理，不过这点我们在之前的直接在仙人掌上动态规划的题目中已经讨论过了；真正麻烦的问题是原始的圆方树上一个方点的所有儿子都是此方点所带白哦的环内的点，但是建完圆方树的虚树之后就不是这样了，而我们之前的动态规划方法都是基于环的。其实处理方法也很简单：对于方点 $u$ 的一个不在方点所代表的环上的儿子 $v$ ，找到 $v$ 的一个祖先 $x$ ，使 $x$ 在 $u$ 所代表的环上即可，如图所示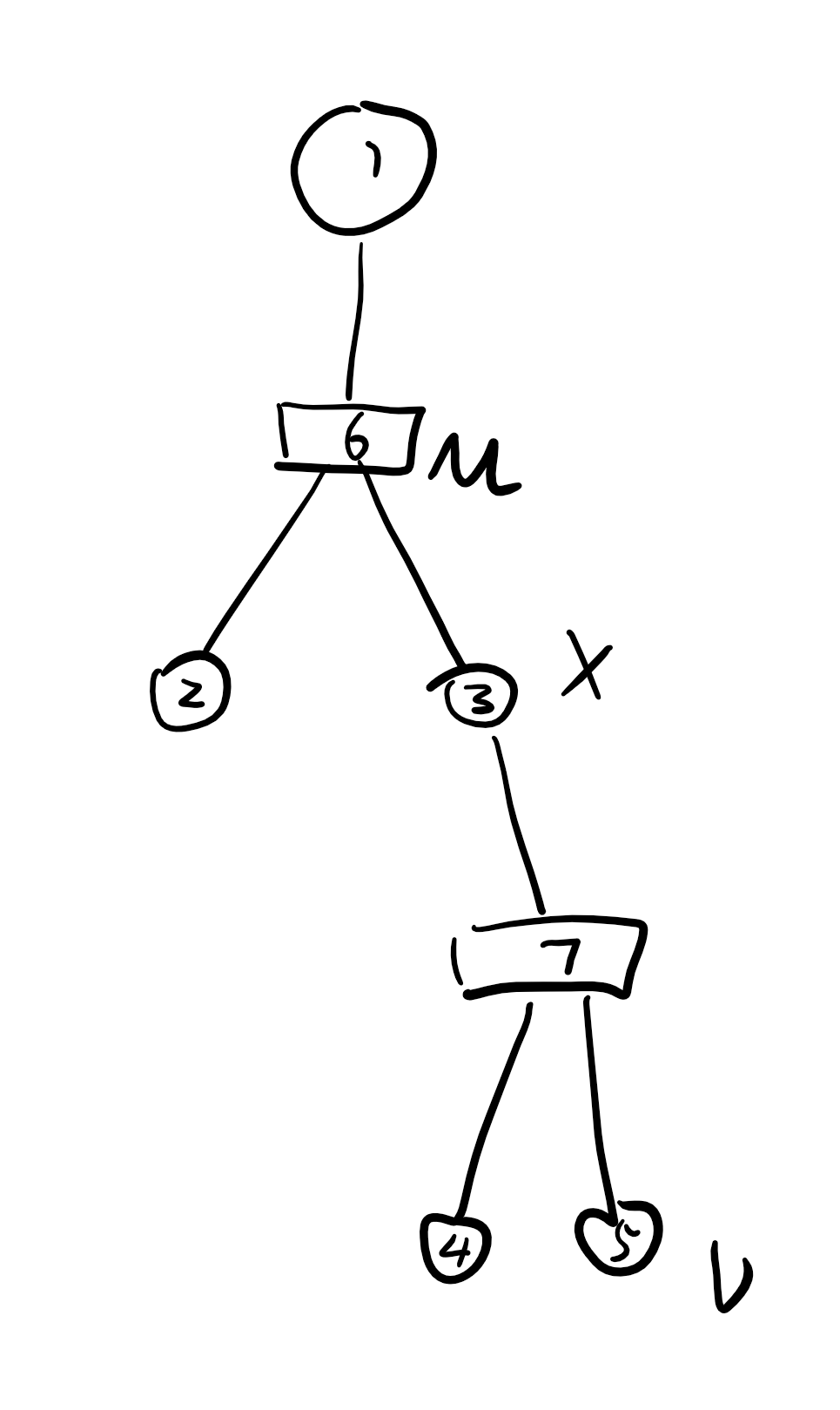：117340074aaf0e6f849a2.png

[UOJ87] mx的仙人掌

给定一棵 $n$ 个点 $m$ 条边的带权仙人掌，有 $q$ 次询问，每次询问一个点集中的点的最短路的最大值，询问点数之和为 $tot$。

$n,q,tot\leq3\times10^5$

与 BZOJ1023 十分相似，按照虚仙人掌的套路直接动态规划就好，本题的难点其实在于重边的处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<map>
#include<algorithm>
using std::min;
using std::max;
typedef long long ll;

const int MAXN=6e5+5;

int N,ncnt,M,Q,CNT;

ll A(int u,int v){return 1LL*u*MAXN+1LL*v;}
std::map<ll,ll> W[2];
struct E{int next,to;} e[MAXN<<3];int ecnt,G[2][MAXN];
void addEdge(int t,int u,int v,ll w=-1)
{
	if(u==v) return;
	if(~w)
	{
		if(W[t].count(A(u,v))) {W[t][A(u,v)]=min(W[t][A(u,v)],(ll)w);return;}
		W[t][A(u,v)]=w;
	}
	e[++ecnt]=(E){G[t][u],v};G[t][u]=ecnt;
}
void addEdge2(int t,int u,int v,ll w=-1){addEdge(t,u,v,w);addEdge(t,v,u,w);}

std::stack<int> st;
ll ringDis[MAXN],rLen[MAXN];
int dfn[MAXN],low[MAXN],dcnt;
void tarjan(int u,int la)
{
	st.push(u);
	dfn[u]=low[u]=++dcnt;
	for(int i=G[0][u];i;i=e[i].next)
	{
		int v=e[i].to;
		if(v==la) continue;
		if(!dfn[v])
		{
			ringDis[v]=ringDis[u]+W[0][A(u,v)];
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
			if(dfn[u]<=low[v])
			{
				rLen[++ncnt]=ringDis[st.top()]-ringDis[u]+W[0][A(u,st.top())];
				while(true)
				{
					int t=st.top();st.pop();
					addEdge(1,ncnt,t,min(ringDis[t]-ringDis[u],rLen[ncnt]-ringDis[t]+ringDis[u]));
					if(t==v) break;
				}
				addEdge(1,u,ncnt,0);
			}
		}else low[u]=min(low[u],dfn[v]);
	}
}

ll rtDis[MAXN];
int anc[MAXN][20];
int dpt[MAXN];
void dfs(int u)
{
	int i;dfn[u]=++dcnt;
	for(i=1;(1<<i)<=dpt[u];i++)
		anc[u][i]=anc[anc[u][i-1]][i-1];
	for(i=G[1][u];i;i=e[i].next)
	{
		int v=e[i].to;
		dpt[v]=dpt[u]+1;
		anc[v][0]=u;
		rtDis[v]=rtDis[u]+W[1][A(u,v)];
		dfs(v);
	}
}
void jmp(int &x,int tgt)
{
	for(int i=19;i>=0;i--)
		if(dpt[x]-(1<<i)>=tgt)
			x=anc[x][i];
}
inline int calLCA(int x,int y)
{
	int i;if(dpt[x]<dpt[y]) std::swap(x,y);
	jmp(x,dpt[y]);
	if(x==y) return x;
	for(i=19;i>=0;i--)
		if(anc[x][i]!=anc[y][i])
			x=anc[x][i],y=anc[y][i];
	return anc[x][0];
}

int seq[MAXN],scnt;
bool cmp(int a,int b){return dfn[a]<dfn[b];}
void buildTree()
{
	int i;ecnt=0;
	std::sort(seq+1,seq+1+CNT,cmp);CNT=std::unique(seq+1,seq+CNT+1)-(seq+1);
	static int st[MAXN],tp;
	st[tp=1]=1;
	for(i=1;i<=CNT;i++)
	{
		int lca=calLCA(seq[i],st[tp]);
		while(dpt[st[tp-1]]>dpt[lca]) {addEdge(1,st[tp-1],st[tp]);tp--;}
		addEdge(1,lca,st[tp]);tp--;
		if(st[tp]!=lca) st[++tp]=lca;
		if(st[tp]!=seq[i]) st[++tp]=seq[i];
	}
	while(--tp) addEdge(1,st[tp],st[tp+1]);
}

ll ans,f[MAXN];
ll rF[MAXN<<1],rD[MAXN<<1];
int dq[MAXN];
inline void wrk(int r)
{
	int i,hd,tl;
	for(i=1;i<=scnt;i++) rF[i]=f[seq[i]],rD[i]=ringDis[seq[i]];
	rD[scnt+1]=rD[1]+rLen[r],rF[scnt+1]=rF[1];
	for(i=scnt+2;i<=scnt<<1;i++)
		rD[i]=rD[i-1]+rD[i-scnt]-rD[i-scnt-1],rF[i]=rF[i-scnt];
	dq[hd=tl=1]=1;
	for(i=2;i<=2*scnt;i++)
	{
		while(hd<=tl&&2*rD[i]>rLen[r]+2*rD[dq[hd]]) hd++;
		if(hd<=tl) ans=max(ans,rD[i]-rD[dq[hd]]+rF[i]+rF[dq[hd]]);
		while(hd<=tl&&rF[i]-rD[i]>=rF[dq[tl]]-rD[dq[tl]]) tl--;
		dq[++tl]=i;
	}
}

bool vis[MAXN];
void trDP(int u)
{
	int i;f[u]=0;
	if(u>N)
	{
		for(i=G[1][u];i;i=e[i].next)
			trDP(e[i].to);
		scnt=0;
		for(i=G[1][u];i;i=e[i].next)
		{
			int v=e[i].to;
			f[u]=max(f[u],f[v]+rtDis[v]-rtDis[u]);
			int x=v;jmp(x,dpt[u]+1);
			f[x]=f[v]+rtDis[v]-rtDis[x];
			seq[++scnt]=x;
		}
		std::reverse(seq+1,seq+1+scnt);
		wrk(u);
	}
	else
		for(i=G[1][u];i;i=e[i].next)
		{
			int v=e[i].to;
			trDP(v);
			if(vis[u]) ans=max(ans,f[u]+f[v]+rtDis[v]-rtDis[u]);
			f[u]=max(f[u],f[v]+rtDis[v]-rtDis[u]);
			vis[u]=true;
		}
	G[1][u]=0,vis[u]=false;
}

const int rt=1;
int main()
{
	int i;
	scanf("%d%d",&N,&M);ncnt=N;
	for(i=1;i<=M;i++)
	{
		int u,v,w;scanf("%d%d%d",&u,&v,&w);
		addEdge2(0,u,v,w);
	}
	tarjan(rt,0);
	dcnt=0;
	dfs(rt);
	memset(G[1],0,sizeof G[1]);
	int Q;scanf("%d",&Q);
	while(Q--)
	{
		scanf("%d",&CNT);
		for(i=1;i<=CNT;i++) scanf("%d",seq+i),vis[seq[i]]=true;
		buildTree();
		ans=0;
		trDP(rt);
		printf("%lld\n",ans);
	}
	return 0;
}

仙人掌点分治

动态仙人掌