##A 彩虹溜冰鞋
有一个 $R\times C$ 的循环网格地图(即走出上边界的上方为下边界,以此类推),给定一个起点 $(I,J)$ 。在上面走 $N$ 步,初始时面向正上方,走第 $i$ 步时向前走 $i$ 步,然后顺时针转 $90^\circ$ 。初始时颜色为 ‘ A ‘ ,之后没一步的颜色循环地分配下一个字母( ‘ Z ‘ 后面是 ‘ A ‘),每一步走过的路径前必后开得染上当前的颜色。问最后的颜色状态。
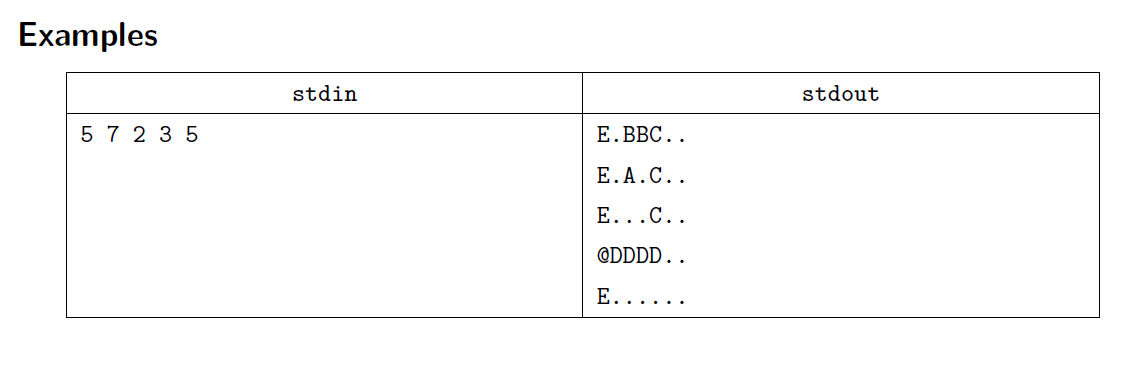
$R,C\leq2000,N\leq10^{18}$
看到 $N$ 的数据范围就知道本题的复杂度肯定与输出同阶了。
发现当 $N$ 很大时,每走一步一定是可以覆盖一行或者一列的,那么影响最后的颜色状态的步数大概与 $R+C$ 同阶 。
于是我们就暴力模拟最后的步数,直到所有位置都染上颜色为止。
至于如何模拟,最重要的就是求出每一步结束的位置,推一波公式:
$$
\left{
\begin{aligned}
r_i&=I+(-1)^{\left\lfloor \frac{i-1}{2}\right\rfloor}\left(\left\lfloor \frac{i-1}{2}\right\rfloor+1\right)\
c_i&=J+(-1)^{\left\lfloor \frac{i+2}{2}\right\rfloor}2\left\lfloor \frac{i+2}{4}\right\rfloor
\end{aligned}
\right.
$$
之后就随手模拟喽。
1 |
|
B 线段树的匹配
一棵树的匹配是指一个树边集合,使得任意两条边没有公共端点。给定一个区间长度 $n$ ,求维护这个区间的线段树的最大匹配种类数。答案对 $998244353$ 取模。
$n\leq10^{18}$
注意到线段树是一个递归结构,对于固定的区间长度来说线段树的形态是固定的,那么最大匹配的种类数就是固定的了。维护长度为 $n$ 的区间的线段树最多有 $\log_2n$ 种形态,记忆化搜索即可。
1 |
|